Por que um problema simples é um dos buracos negros da matemática:como ganhar nas apostas esportivas
Crédito, Pokipsy76
"Mapa fractalcomo ganhar nas apostas esportivasCollatz na vizinhançacomo ganhar nas apostas esportivasuma reta real" - belo mas indecifrável, sobretudo para quem não conhece a matemática
como ganhar nas apostas esportivas Simples não significa fácil.
E este problema, um dos buracos negros da matemática, é prova disso.
Ele começa dando muitas possibilidadescomo ganhar nas apostas esportivascomo chamá-lo: talvez a denominação mais comum seja conjecturacomo ganhar nas apostas esportivasCollatz,como ganhar nas apostas esportivasreferência ao matemático alemão Lothar Collatz, o primeiro a propô-lo,como ganhar nas apostas esportivas1937.
Mas é possível encontrá-lo como conjecturacomo ganhar nas apostas esportivasUlam (pelo matemático polonês-americano Stanisław Marcin Ulam), problemacomo ganhar nas apostas esportivasKakutani (pelo matemático nipo-americano Shizuo Kakutani), conjecturacomo ganhar nas apostas esportivasThwaites (pelo acadêmico britânico Bryan Thwaites), algoritmocomo ganhar nas apostas esportivasHasse (pelo matemático alemão Helmut Hasse) ou problemacomo ganhar nas apostas esportivasSiracusa.
E não é tudo: a sequênciacomo ganhar nas apostas esportivasquestão também pode ser chamadacomo ganhar nas apostas esportivasnúmeroscomo ganhar nas apostas esportivasgranizo ou números maravilhosos.
O nome mais descritivo talvez seja conjecturacomo ganhar nas apostas esportivas3n + 1.
Simplicidade complexa
Mas não é isso que desafia os matemáticos: seja qual for o nome, continua sendo o problema impossível mais simplescomo ganhar nas apostas esportivastodos.
Qualquer pessoa que saiba somar, dividir e multiplicar pode entender do que se trata, seguir a sequênciacomo ganhar nas apostas esportivasnúmeros e até tentar resolvê-lo.
Desde os anos 1930, contudo, ninguém conseguiu explicá-lo, prová-lo ou refutá-lo.
Em algum momento especulou-se que a conjectura pudesse ser uma estratégia soviética para distrair os cientistas.
Deste modo, antescomo ganhar nas apostas esportivasapresentar o problema, vale lembrar uma advertênciacomo ganhar nas apostas esportivasum dos matemáticos mais produtivos - e excêntricos - do século 20:
A matemática não está pronta para este tipocomo ganhar nas apostas esportivasproblema (...) Absolutamente impossível."
Eis o problema:
Comece com um número natural inteiro qualquer (1, 2, 3, 4, 5...).
- Se o número é par, divida-o por 2
- Se é ímpar, multiplique-o por 3 e some 1
Depois aplique essas mesmas regras simples ao resultado.
Comecemos com 10, que é par.
10 ÷ 2 = 5, que é ímpar, então aplicamos a segunda regra.
5 x 3 = 15 + 1 = 16.
Como é par... 16 ÷ 2 = 8
8 ÷ 2 = 4
4 ÷ 2 = 2
2 ÷ 2 = 1
Até aqui, simples.
O que torna o problema intrigante é que não importa com qual número comece, eventualmente sempre chegará a 4, que se convertecomo ganhar nas apostas esportivas2 e terminacomo ganhar nas apostas esportivas1.
Pelo menos é esse o caso com todos os números que foram testados, e já se tentou usar alguns quase absurdos.
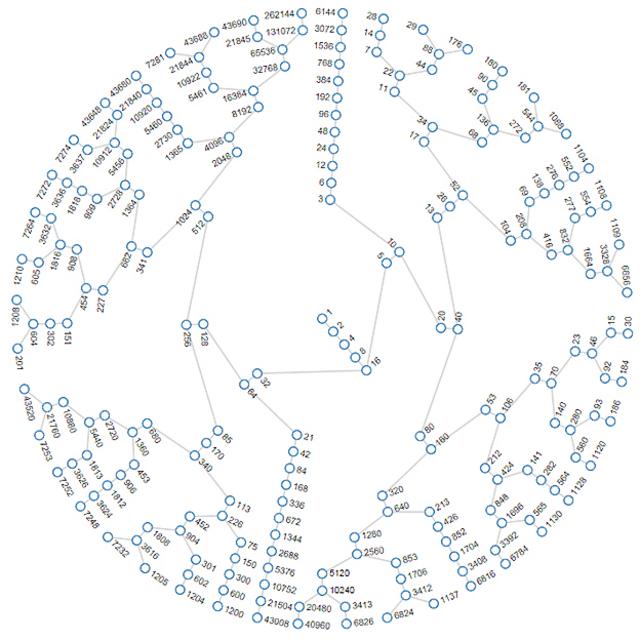
Crédito, Jason Davies
Jason Davies, programador que faz excelentes visualizaçõescomo ganhar nas apostas esportivasdados, criou um gráfico sobre a conjecturacomo ganhar nas apostas esportivasCollatz: todos os números levam ao 1.
Supercomputadores fizeram o problema com números que vão até aproximadamente 5.764.607.500.000.000.000.
Todos eventualmente chegam a 2 ÷ 2 = 1.
Contudo, como os números são infinitos, isso não prova que esse seja o caso para todos os números naturais.
Mas como não se encontrou uma exceção, tampouco há provascomo ganhar nas apostas esportivasque não seja assim.
Outra questão é resolver o eterno por quê. Por que os números se comportam assim?
Devo avisá-los que não tentem resolvê-lo na mente ou calculá-lo na partecomo ganhar nas apostas esportivastráscomo ganhar nas apostas esportivasum velho envelope."
Granizo
O problema chega sempre ao mesmo ponto, não importa como.
A confusão é que na horacomo ganhar nas apostas esportivasresolvê-lo desenhando um algoritmo (sequência finitacomo ganhar nas apostas esportivasregras, raciocínios ou operações que permite solucionar classes semelhantescomo ganhar nas apostas esportivasproblemas), há pedrascomo ganhar nas apostas esportivasgelo no caminho.
Como o granizo nas nuvens antescomo ganhar nas apostas esportivascair, os números saltamcomo ganhar nas apostas esportivasum lugar ao outro antescomo ganhar nas apostas esportivaschegar ao 4, 2, 1.
Uns mais e outros menos, sem sentido aparente.
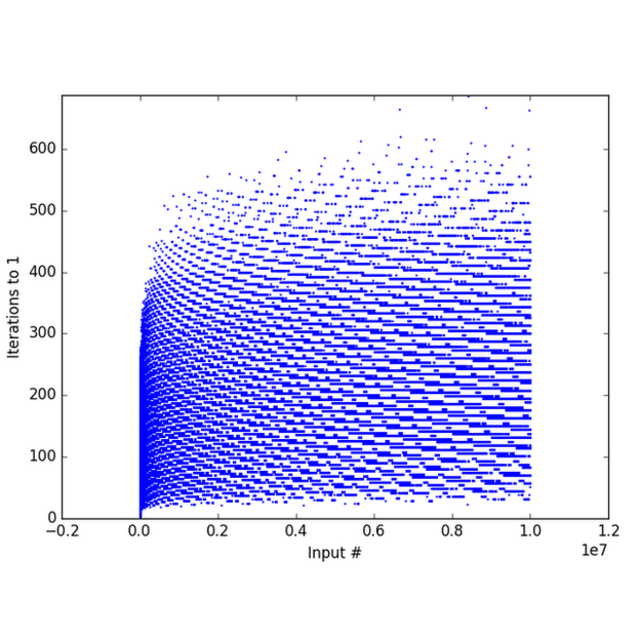
Crédito, Kunashmilovich - Creative Commons
Iterações necessárias para chegar a 4, 2, 1 para os númeroscomo ganhar nas apostas esportivas2 a 10.000.000
A maior quantidadecomo ganhar nas apostas esportivasescalas que faz um número inicial menorcomo ganhar nas apostas esportivas100 milhões para chegar a 4, 2, 1 é 986.
Mas enquanto a "viagem" é mais curta para os múltiploscomo ganhar nas apostas esportivas2, outros levam mais tempo.
Um exemplo citado com frequência é a comparação entre os números 8.192 e 27.
O 8.192 leva 13 passos para chegar ao final aparentemente inescapável: 4, 2, 1.
O número 27 não apenas leva 111 passos para chegar, mas no caminho sobe até 9.232 antescomo ganhar nas apostas esportivaspoder alcançar o 4, 2, 1.
A ausênciacomo ganhar nas apostas esportivaspadrões dificulta ainda mais resolver uma conjectura já classificada como impossível.
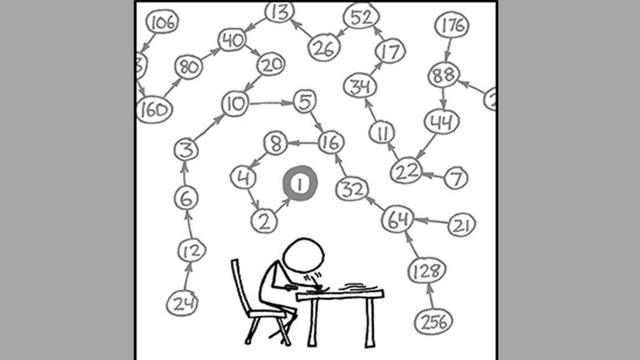
Crédito, XKCD.COM
Se o problema é quase impossível, vale a pena continuar tentando desvendá-lo?
Curioso e relevante?
Se o problema é tão difícil, e talvez impossível, vale a pena continuar tentando resolvê-lo?
"Quando passar dias ou semanas tentando,como ganhar nas apostas esportivasvão, resolver um problema, pense no pobre Sísifo e emcomo ganhar nas apostas esportivaspedra", aconselhou o geometrógrafo Coxeter.
"Como (o matemático alemão) Felix Behrend diz ao finalcomo ganhar nas apostas esportivasseu livro, 'Sísifo ecomo ganhar nas apostas esportivaspedra são símbolos do homem ecomo ganhar nas apostas esportivassua eterna luta, incessante, inalcançável e, contudo, sempre triunfal. O que mais se pode pedir?'"
Poético, mas se isso não o convence sobre a importânciacomo ganhar nas apostas esportivasesclarecer esse mistério, recorramos aos especialistas do Mathematics Stack Exchange, sitecomo ganhar nas apostas esportivasperguntas e respostas para pessoas que estudam matemáticacomo ganhar nas apostas esportivasqualquer nível e profissionaiscomo ganhar nas apostas esportivasáreas relacionadas.
"Os matemáticos suspeitam que solucionar a conjecturacomo ganhar nas apostas esportivasCollatz abrirá novos horizontes e desenvolverá novas e importantes técnicas na teoria dos números", disse Greg Muller.
"O problemacomo ganhar nas apostas esportivasCollatz é suficientemente simples para que qualquer pessoa o entenda, e não se relaciona apenas com a teoria dos números, mas com problemascomo ganhar nas apostas esportivasdecidibilidade, o caos e com fundamentos da matemáticacomo ganhar nas apostas esportivascomputação. Melhor impossível", escreveu o usuário Matt.
"Outra razão é que, por ser fácilcomo ganhar nas apostas esportivasapresentar e entender, tem potencialcomo ganhar nas apostas esportivasatrair jovens para a matemática. Eu mesmo soubecomo ganhar nas apostas esportivassua existência no ensino médio e não resisti a seu encanto", comentou Derek Jennings.