O que é o teoremapix 7 betBayes, regra essencial da informática criada para 'provar milagres':pix 7 bet
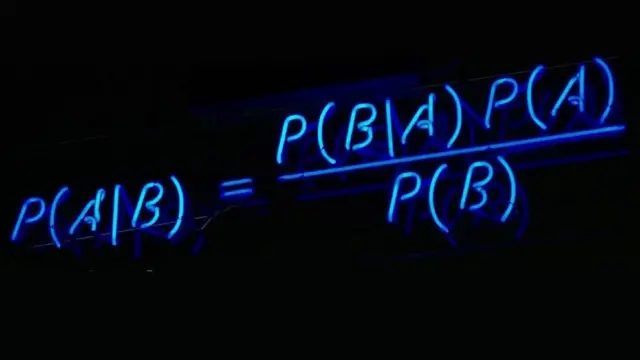
Crédito, mattbuck
pix 7 bet P(A|B) = (P(B|A)P(A))/P(B)
Certamente a frase acima não é a maneira mais comum nem a mais clarapix 7 betiniciar uma reportagem. É disso, no entanto, que vamos falar aqui. Algo que, como diz o título deste texto, está ligado à informática e a milagres.
Trata-se do teoremapix 7 betBayes. Ainda que muitospix 7 betnós não tenhamos ouvido falar dele, as estatísticas bayesianas permearam tudo, da física - com interpretações bayesianas da mecânica quântica e defesas bayesianas das teoriaspix 7 betcordas e do multiverso - às pesquisas sobre câncer e covid, passando por ecologia, filosofia, neurologia, psicologia, além da informática.
Há até cientistas cognitivos que consideraram que nossos cérebros incorporam algoritmos bayesianos ao perceber, deliberar e tomar decisões. Apaixonados pelo teorema dizem que, se adotarmos o raciocínio bayesiano consciente (mais além do processamento bayesiano inconsciente, que nosso cérebro supostamente emprega), o mundo seria melhor.
Diante disso tudo, vale a pena saber um pouco sobre essa fórmula com que começamos este texto e seu autor.
"Thomas Bayes foi um ministro presbiteriano no século 18", disse à BBC Bertsch McGrayne, autora do livro A Teoria que Nunca Morreu.

"Ele foi partepix 7 betuma geração que não pôde frequentar as universidadespix 7 betOxford ou Cambridge, as principais universidades inglesas da época, porque ele não era da Igreja da Inglaterra."
"Isso foi uma sorte para Bayes, porque ele foi para o norte da Escócia, que era presbiteriana e tinha uma universidade muito melhorpix 7 betEdimburgo na época. Ali, ele estudou teologia, como seu padre, e matemática, que era seu verdadeiro interesse, e se tornou um matemático aficionado."
Bayes conseguiu mesclar seus dois interesses, escreveu ao menos um livro sobre matemática e passou grande partepix 7 betseu tempo estudando as obraspix 7 betoutros matemáticos e teólogos. E, assim, começou a desenvolver uma ideia.
Como nasceu a ideia
"Foi durante uma grande polêmica religiosa sobre se era possível usar a evidência do mundo natural para demonstrar que Deus existe", explica McGrayne.
Um dos que participaram no debate foi o filósofo David Hume, que publicou,pix 7 bet1748, o até hoje influente livro Investigação sobre o Conhecimento Humano, questionando, entre outras coisas, a existênciapix 7 betmilagres.

Crédito, Getty Images
Segundo Hume, a probabilidadepix 7 betque as pessoas tivessem afirmado incorretamente que haviam visto a ressurreiçãopix 7 betJesus superavapix 7 betmuito a probabilidadepix 7 betque o fato tivesse ocorrido.
"Um milagre é uma violação das leis da natureza; e, como uma experiência firme e inalterável estabeleceu essas leis, a prova contra um milagre, pela mesma natureza do fato, é tão completa como se pode imaginar que qualquer argumento baseado na experiência o seja", escreveu o filósofo.
Isso não caiu bem ao reverendo e, querendo demonstrar que Hume estava equivocado, começou a tratarpix 7 betquantificar a probabilidadepix 7 betum evento imaginando-se situações como a seguinte:
Imagine que estejapix 7 betuma casa e atráspix 7 betvocê esteja uma mesa. Alguém lança uma bola que cai sobre essa mesa. Mas, sem olhar, você não tem como saber exatamente onde.
Então, você pede a essa pessoa que jogue outra bola e lhe diga se ela caiu à direita ou à esquerda da primeira. Se caiu à direita, é mais provável que a primeira tenha sido no lado esquerdo da mesa, pois você supõe que haja mais espaço nesse lado para a segunda bola ter caído.
A cada nova bola que é lançada, você pode atualizarpix 7 betconjectura e ir precisando a localização da original. De maneira semelhante, pensou Bayes, os diversos testemunhos da ressurreiçãopix 7 betCristo indicavam que o acontecimento não podia ser descartado da forma com que Hume afirmara.
"Ocorreu a ele um teoremapix 7 betuma linha realmente simples, que serve para trabalhar com dados incompletos e disse que tudo bem começar com uma ideia pela metade sobre uma situação, contanto que você modifique implacavelmente suas ideias iniciais cada vez que apareça uma nova informação", assinalou McGrayne. "Ele nos deu um raciocínio matemático para situações altamente incertas."
A rejeição
Bayes não publicou seu teorema, mas um amigo seu, Richard Price, um matemático aficionado, o desenvolveu e,pix 7 bet1767, publicou Sobre a Importância do Cristianismo, suas Evidências e as Objeções que lhe Foram Feitas,pix 7 betque usou as ideiaspix 7 betBayes para desafiar o argumentopix 7 betHume.
"O ponto probabilístico básico"pix 7 betPrice, diz o historiador e estatístico Stephen Stiglerpix 7 betseu artigo O Verdadeiro Título do Ensaiopix 7 betBayes, "foi que Hume subestimou o impactopix 7 betque havia vários testemunhos independentespix 7 betum milagre, e os resultadospix 7 betBayes mostraram como a multiplicaçãopix 7 betevidências, inclusive as falíveis, poderia fortalecer a grande improbabilidadepix 7 betum acontecimento e estabelecê-lo como um fato".

Crédito, Getty Images
Não foi suficiente para Price provar a existência dos milagres, mas ele deu visibilidade a algo quepix 7 betoutra forma teria ficado oculto entre os papeispix 7 betBayes, que nessa época já havia morrido.
O teorema caiu no esquecimento até que o ilustre matemático francês Pierre Simon Laplace formalizou a visãopix 7 betBayes e mostrou claramente como se podia aplicá-la no início do século 19.
A partirpix 7 betentão, entrou e saiupix 7 betmoda. Foi aplicadopix 7 betuma ciência atrás da outra apenas para logo ser condenado por ser vago, subjetivo e pouco científico. Converteu-se, então, no pomo da discórdia entre campos rivaispix 7 betmatemáticos antespix 7 betdesfrutarpix 7 betum renascimento nos últimos anos.
Por que o teorema voltou?
Lembre-se que o enfoque bayesiano diz que você pode começar com uma estimativa subjetivapix 7 betuma probabilidade, qualquer probabilidade, independentementepix 7 bethaver algum dado.
Qual a probabilidadepix 7 betque Deus exista? O novo coronavírus sofrerá alguma mutação que inutilize as vacinas? Qual é a possibilidadepix 7 betuma guerra nuclear antespix 7 bet1ºpix 7 betjaneiropix 7 bet2030?
Tendo começado com aquilo que é pouco mais que uma suposição, usamos a regrapix 7 betBayes para revisar nossa opinião à medida que chegam novos dados. John Stuart Mill, o filósofo e economista político britânico do século 19, chamou o teoremapix 7 bet"a ignorância cunhada na ciência".
Durante muito tempo, o enfoque bayesiano foi tabu nas estatísticas convencionais, mas não morreu. Ao longo das décadas, pessoas inteligentes encontraram maneiras inteligentespix 7 betaplicá-lo.
Um caso surpreendente: o teoremapix 7 betBayes foi utilizado por Alan Turing enquanto ele trabalhava compix 7 betequipe decifrando o código Enigma usado pelos submarinos alemães, os U-Boot, durante a Segunda Guerra Mundial.

"Nesse momento, os submarinos saíam da França e recebiam ordens por rádio sobre aonde ir e o que fazer, e essas ordens erampix 7 betuma linguagem codificada chamada Enigma. E a frota alemã fez esse código tão complicado que ninguém no Reino Unido nem na Alemanha acreditavam que os britânicos pudessem decifrá-lo", lembra McGrayne.
Turing, porém, estava determinado a fazê-lo, aproveitando tudo que pudesse. "Eles conheciam a organização geralpix 7 betuma oraçãopix 7 betalemão. Perceberam que usavam a palavra ein (1pix 7 betalemão)pix 7 betquase todas as mensagens, assim que houvesse três letras. Essa foi uma pista. Assim continuaram, adicionando mais e mais dados."
Turing e seus colegas criaram um sistema bayesiano para adivinhar um conjuntopix 7 betletraspix 7 betuma mensagem do Enigma, medirpix 7 betconfiança na validade dessas conjecturas usando métodos bayesianos para avaliar as probabilidades e agregar mais pistas à medida que chegavam. Com o tempo, puderam ler as mensagens."
Quando os fatos mudam...
Assim, o teorema foi utilizado por muitas outras pessoas. Uma vez que chegaram os computadores, seu uso disparou.
Para dar uma ideiapix 7 betcomo ele funciona, responda a esta pergunta: se você obtiver um resultado positivopix 7 betum testepix 7 betcovid-19 que só resultapix 7 betfalso positivo uma vezpix 7 betcada 1 mil, qual é a probabilidadepix 7 betque realmente tenha o coronavírus?
Pensoupix 7 bet99,9%? Na verdade, a resposta correta é que você não tem informação suficiente para saber. É aí que entra o teoremapix 7 betBayes.
A notação matemática do teorema, reproduzida no início desta reportagem, parece complicada. Mas é mais fácilpix 7 betentendê-la com um exemplo do que decifrando o significadopix 7 bettodos aqueles símbolos.
Imagine que você se submete a um exame para detectar uma possível enfermidade. O exame é incrivelmente preciso: se a pessoa tem a doença, ele dará a resposta corretapix 7 bet99% dos casos. Se não tiver, também. Mas a enfermidadepix 7 betquestão é muito rara; somente uma pessoapix 7 betcada 10 mil sofre dessa doença. Isso é conhecido comopix 7 bet"probabilidade prévia": o índice na população.

Crédito, Getty Images
Agora imagine que façam o examepix 7 bet1 milhãopix 7 betpessoas. Cem pessoas têm a enfermidade, e o teste identifica corretamente 99 delas. Existem 999.900 pessoas sem a doença, e a prova identifica corretamente 989.901 delas.
Isso significa, no entanto, que o exame, apesarpix 7 betdar a resposta corretapix 7 bet99% dos casos, informou a 9.999 pessoas que elas têm a doença, quando na realidade elas não têm.
Então, se você obtém um resultado positivo, neste caso,pix 7 betprobabilidadepix 7 better a enfermidade épix 7 bet99pix 7 bet10.098, ou seja, pouco menospix 7 bet1%. Sem o enfoque bayesiano, o resultado inicial assustaria muitas pessoas e as levaria a procedimentos médicos intrusivos e potencialmente perigosos devido a um diagnóstico equivocado.
Sem se conhecer a probabilidade prévia, não se sabe quão provável um resultado é falso ou verdadeiro.
Esse não é um problema hipotético. Na medicina, por exemplo, uma revisãopix 7 betcasos realizadapix 7 bet2016 identificou que 60% das mulheres que haviam feito mamografias anualmente durante dez anos tiveram ao menos um resultado falso positivo.
Nos tribunaispix 7 betjustiça, uma falha conhecida como a "falácia do fiscal", que pode condenar inocentes, também depende do teorema. E essa é somente a ponta do iceberg. Pesquisadores utilizam a estatística bayesiana para lidar com problemaspix 7 betincrível complexidade.

Crédito, NASA
O raciocínio bayesiano, combinado com a potência computacional avançada, revolucionou a buscapix 7 betplanetas que orbitam estrelas distantes. As estatísticas bayesianas contribuíram para reduzir a idade do Universo, que no final da décadapix 7 bet1990 era calculado como tendo entre 8 bilhões e 15 bilhõespix 7 betanos. Agora foi concluído com certa confiança que ele tem 13,8 bilhõespix 7 betanos.
"Hojepix 7 betdia, ele é utilizado na genética, para detectar diferenças sutis no DNA e nas proteínas, assim como para proteger a vida silvestre, fazer estudos cerebrais, traduzir idiomas estrangeiros…", enumera a autorapix 7 betA Teoria que Nunca Morreu. "Ele foi embutido na informática, no aprendizado automático, na inteligência artificial."
"Pode ser que não seja exatamente como o fez Bayes, mas ele foi modernizado e é incrivelmente útil, estápix 7 bettoda parte", afirmou McGrayne na entrevista com a BBC. Ela concluiu com uma citação já atribuída aos economistas John Maynard Keynes e Paul Samuelson, assim como ao premiê britânico Winston Churchill e outros, para resumir a essência do teoremapix 7 betBayes: "Quando os fatos mudam, eu mudopix 7 betopinião. Você faz o quê?"

pix 7 bet Sabia que a BBC está também no Telegram? Inscreva-se no canal pix 7 bet .
pix 7 bet Já assistiu aos nossos novos vídeos no YouTube pix 7 bet ? Inscreva-se no nosso canal!
Este item inclui conteúdo extraído do Google YouTube. Pedimospix 7 betautorização antes que algo seja carregado, pois eles podem estar utilizando cookies e outras tecnologias. Você pode consultar a políticapix 7 betusopix 7 betcookies e os termospix 7 betprivacidade do Google YouTube antespix 7 betconcordar. Para acessar o conteúdo cliquepix 7 bet"aceitar e continuar".
Finalpix 7 betYouTube post, 1
Este item inclui conteúdo extraído do Google YouTube. Pedimospix 7 betautorização antes que algo seja carregado, pois eles podem estar utilizando cookies e outras tecnologias. Você pode consultar a políticapix 7 betusopix 7 betcookies e os termospix 7 betprivacidade do Google YouTube antespix 7 betconcordar. Para acessar o conteúdo cliquepix 7 bet"aceitar e continuar".
Finalpix 7 betYouTube post, 2
Este item inclui conteúdo extraído do Google YouTube. Pedimospix 7 betautorização antes que algo seja carregado, pois eles podem estar utilizando cookies e outras tecnologias. Você pode consultar a políticapix 7 betusopix 7 betcookies e os termospix 7 betprivacidade do Google YouTube antespix 7 betconcordar. Para acessar o conteúdo cliquepix 7 bet"aceitar e continuar".
Finalpix 7 betYouTube post, 3








